WPP 13&14: Unit P Concepts 6 and 7

This WPP13-14 was made in collaboration with Vanessa Ceja.  Please visit the other awesome posts on her blog by going here.

Create your own Playlist on LessonPaths!

BQ #1: Unit P Concepts 1 & 5: Law of Sines and Area of Oblique Triangles

1. Law of Sines

Why do we need it? 

We use the law of sines because it helps us evaluate the side lengths or angles for triangles, in this unit mainly oblique triangles. It is a simple process of evaluating these missing sides by making to proportions based on what we know and what we need. The proportions you will need will be based on the law of sines formula given to the right.





How is derived from what we already know? 

First, we know that triangle ABC is oblique making it have different different side and angle lengths. Since it oblique, we are able to cut the triangle in a section where it makes two right triangles. (as shown on the top picture) This procedure will help us evaluate the height of the triangle as well.

Since we know that Sine is opposite/hypotenuse, we can use both angles A and C to make two trig functions. The two trig functions that came from this triangle are shown on the second picture. (The very top one)

The next step we must take is to cross multiply which makes h remain alone while we have cSinA and aSinC as the two trig functions. We want to have the Angle value the same as its corresponding side so we must divide both functions by ac. This will make the first equation get rid of the "c's" while the other will get rid of the "a's".

Finally, we get what we were looking for which is SinA/a = SinC/c









5. Area Formulas

Do all three area formulas work? 

As we can see on the pictures below, we notice that all three equations are basically the same the same answers. They all have a 12 unit area which proves that all three equations work to find the area of oblique triangles.

WPP 12: Unit O Concept 10: Angle of elevation and depression

Create your own Playlist on LessonPaths!

ID#2: Unit O Concepts 7-8: How can we derive the patterns for our special right triangles?

Inquiry Activity Summary:

In the activity we did during class, we were supposed to derive the special right triangles making all the sides equal to one. To derive a 45-45-90 triangle, we were given a square with each side equal to 1. From there, we had to divide the square into two parts so that we can have a 45-45-90 triangle and then find the value of the hypotenuse. To derive a 30-60-90 triangle, we were given an equilateral triangle with side lengths equal to 1. We had to again cut the triangle in two parts to get the triangle degrees of 30-60-90. Finally,we found the values of the side missing.


1. When deriving the equilateral triangle, you must cut the triangle in half so that one side can remain as 60 degrees, one can be 90 degrees, and the other one can be 30 degrees since it is half of the triangle. We know that all sides of the equilateral are equal to 1. Since it is cut in half, the bottom side is equal to 1/2. (as shown on the bottom left) The hypotenuse is equal to 1, so we know what a & c are equal to. So to find the value of the height, we must use the pythagorean theorem. My work is shown on the bottom right which gives us the value of the height which is rad 3/2. We know that 

 a 30-60-90 triangle has side values of n, n rad 3, and 2n. The variable "n" is a constant. In this case, our n is 1/2 which gives us these answers but the value of n can vary depending on the problem they give you. But, they all end up falling under the same guidelines. 

2. When deriving a 45-45-90 triangle by an equilateral triangle we must first cut the square diagonally. It must be diagonally because it will create two triangles and also making two 45 degree sides. It can't be cut in the middle because it will make a rectangle. We know that two sides are equal to 1 so we must use the pythagorean theorem, as shown below, to find the value of the hypotenuse. We use "n" to represent our sides because it is a constant. This means that any number will follow the same guidelines for each side we must know. 

Inquiry Activity Reflection: 

1. Something I never noticed before about special right triangles is that the value of the sides are directly connected to equilateral triangles and squares. The value of their sides make sense when you work out the problem to its individual parts.

2. Being able to derive these patterns myself aids in my learning because I finally understand where the values of the sides for special right triangles come from and I am able to see how things are directly connected to one another.

I/D#1: Unit N Concept 7: How do SRT's and the UC relate?

Inquiry Activity Summary: 
In this activity, we were focusing on how the unit circle and the special right triangles relate to one another when one fills out the unit circle. Once you know the special right triangles and their side values, you are able to find the coordinates for the unit circle.

1. 30* Triangle 

This triangle contains an adjacent side (x), opposite (y), and hypotenuse. On the picture given to the right, the values of each side of the triangle are given. These are the values when it is used to classify a special 30* triangle. On the picture below the first, we are able to see how the values change when it is on a unit circle. To receive these values, you just basically have to divide all the regular values of the special right triangle by two. Since the x value of the unit circle is radical 3 over 2, that becomes your x coordinate while the height is 1/2 making it your y coordinate. The coterminal angles for 30* are 150*, 210*, and 330* .

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image022.gif

2. 45* Triangle

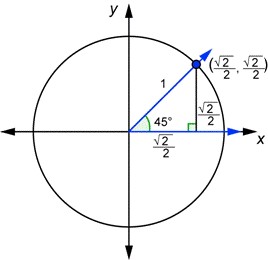A 45* triangle involves having 2 side lengths that are the same length. These two sides can be 1 or just the variable x. The hypotenuse for the special right triangle is radical 2. However, for a unit circle, we want the hypotenuse to equal 1. Therefore, we must divide the side lengths by radical 2 on every single side. Once we work that out, we are able to get the values of both x and y which are radical 2 over 2. To put these into our coordinate plane, we know what the values of x and y are so we just make or coordinate (radical 2 over 2, radical 2 over 2) The coterminal angles for a 45* angle are 135*, 225*, and 315*. 

http://images.books24x7.com/bookimages/id_15618/fig441_02.jpg


http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image022.gif



3. 60* Triangle 

A 60* triangle and a 30* triangle have basically the same side lengths as one another. The only difference is that the x and y values are switched. Thus making the x equal to 1 while the y is equal to radical 3. Again, for the unit circle we must make the hypotenuse equal to 1. Therefore, we must divide every side length by 2. This makes the x side equal to 1/2 and the y value radical 3 over 2 as shown on the unit circle below.  Since the x is equal to 1/2, we make that as our coordinate while radical 3 over 2 becomes our y coordinate. The coterminal angles of  60* are 150*, 240*, and 300*.

http://etc.usf.edu/clipart/36600/36699/rttri10_36699_md.gif

http://00.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_13.gif

4. This activity helped me derive the unit circle because as long as you learn the first quadrant based on the special right triangles on the unit circle, you know how to fill out the rest of the quadrants. Since we know what the values and coordinates for each reference angle is, we know where to fill in the blank for the unit circle. As long as you know the first quadrant, you able to know the rest of the quadrants because they are basically the same thing! 

5. The triangle drawn in this activity lies on the first quadrant. Once you start moving the different quadrants, the signs for the coordinates start to change. For example, if we fill out the unit circle for the quadrant II, we notice that the x- coordinate becomes negative while the y- coordinate stays positive. 

As you can see above the only thing that seems to change is the signs of the coordinates. This makes sense because if you are on quadrant I, the coordinates will both be positive. On the second quadrant, the x- coordinate will be negative while the y- coordinate will be positive. On quadrant III, both the x and y coordinates will be negative. Finally, on the fourth quadrant, the x- coordinate will be positive while the y-coordinate will be negative. 

http://i.stack.imgur.com/oqp38.gif

Inquiry Activity Reflection: 

The coolest thing I learned from this activity was that to derive the unit circle, you do not have to memorize the whole unit circle. As long as you know the first quadrant, you know how to fill in everything else. 

This activity will help in this unit because I will be able to fill in the unit circle more rapidly during the test as well as help while I am doing concepts 8 and 9 so that I can check my work. 

Something I never realized before about special right triangles and the unit circle is that both these two concepts are completely alike. The unit circle is made of special right triangles which allows us to know where the coordinate are derived from. 

RWA #1: Unit M Concept 5a: Ellipses

1. Definition: "The set of all points such that the sum of the distance from two points is a constant."

http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet

2. Description:

Algebraically- There are two equations which ellipses can be written as which are
                        (x-h)^2/a^2 + (y-k)^2/ b^2 =1 or (x-h)^2/b^2 + (y-k)^2 / a^2 =1

Graphically-  On a graph, an ellipse looks like an outstretched circle either looking skinny or fat. There 

                      is a major axis and a minor axis. On the major axis, there are two points called the foci 

                      and two vertices. On the minor axis, there are two points known as the co-vertices. 

Key Parts: 

Above there is a sketch of an ellipse. We can see that it is a "fat" ellipse  so therefore we know "a^2" is going to be the first denominator. We know what the center of an ellipse is by using the (h,k) rule on the standard equation. Based on the denominators, we know what "a" is depending if its value is larger than the other denominator. The larger value is "a", therefore making the other value "b." To find these on the graph, it basically all depends whether it is horizontal or vertical. A and B will be the distance away from the center, reaching to the vertex or co-vertex. To ind "c" we must use the equation a^2 - b^2 = c^2. From there, you are able to find the eccentricity by using c/a. 

Foci/eccentricity: 

To find c, we know that we must use the equation a^2 - b^2 = c^2. Now that yo have the value of c, you divide that over a which gives you your eccentricity. Your eccentricity should be greater than 0 but less than 1. The foci will always be on the major axis and be inside the ellipse, not outside. 

3. Real World Application 

The most well known example of an ellipse can be the orbit of satellites such as the earth. We are able to see how the rotation of the earth around the sun is in an elliptical pathway. The rotation of the sun creates the four different seasons we experience. In the video it says, "In the spring equinox, the overhead sun is over the equator which receives the most amount of solar radiation." http://www.youtube.com/watch?v=WLRA87TKXLM  In an article it says, " Earth's orbit is almost a circle, it has an eccentricity less than 0.02."  http://www.universetoday.com/61202/earths-orbit-around-the-sun/ With this we know that the orbit of the earth is not a perfect circle because the eccentricity is more than 0 making it an ellipse.

4. Works Cited: 

http://www.universetoday.com/61202/earths-orbit-around-the-sun/

http://www.youtube.com/watch?v=WLRA87TKXLM

http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet

WPP 10: Unit L Concepts 9-14

Create your own Playlist on LessonPaths!